Überraschungen mit Haskell
Nebenan beschäftigt man sich mit der Laufzeit von Programmen anhand des Spieles Subtract a Square. Da ich aus einem anderen Projekt heraus in eine ähnliche Situation geriet, möchte ich diese Vorlage hier nutzen. Es geht darum, eine effiziente Methode zu finden, eine größere Menge an Werten systematisch nach verschiedenen Kriterien zu durchsuchen.
Aufgabestellung
Beim Spiel geht es darum, abwechselnd von einer vorgegebenen, positiven Zahl eine Quadratzahl abzuziehen, ohne ins Minus zu rutschen. Wer die letzte positive Zahl abziehen kann, hat gewonnen. Das Spiel endet offensichtlich mit dem Wert 0.
Für derartige Nimm-Spiele gibt es eine allgemeine Gewinnstrategie: Man zieht so, dass der Gegner nicht gewinnen kann.
Dazu tabellarisiert man alle Spiele mit kleineren Startzahlen und schaut, ob man dieses kleinere Spiel gewinnen könnte. Kann man das nicht, hat man eine Verliererposition. Mit der Kenntnis aller kleineren Spielausgänge muss man nur den ersten Spielzug betrachten.
Prozedurale Lösung
Zum Verständnis hier eine prozedurale Lösung des Problems:
with Ada.Text_IO;
with Ada.Command_Line;
procedure SubtractSquare is
function Winners(i : Natural) return Boolean is
type bitfield is array(0 .. i) of Boolean;
pragma Pack(bitfield);
win : bitfield := (0 => False, others => True);
begin
for pos in win'Range loop
for offset in 1 .. pos loop
declare
square : Natural := offset*offset;
begin
exit when square > pos;
if win(pos - square) then
win(pos) := False;
exit;
end if;
end;
end loop;
end loop;
return win(i);
end;
package Cmd renames Ada.Command_Line;
package BIO is new Ada.Text_IO.Enumeration_IO(Boolean);
pos : Positive := Positive'Value(Cmd.Argument(1));
begin
BIO.Put(Winners(pos));
end SubtractSquare;Dieses Programm erzeugt ein (kompaktes) Bitfeld und setzt die Werte von kleinen zu großen Positionen. Der letzte Wert ist dann das gewünschte Ergebnis. Die gewünschte Position wird dem ersten Argument der Kommandozeile entnommen.
$ gnatmake -O2 subtractsquare.adb ada -c -O2 subtractsquare.adb gnatbind -x subtractsquare.ali gnatlink subtractsquare.ali -O2 $ ./subtractsquare 9 FALSE
Soweit so einfach.
Die Laufzeit ist maximal quadratisch (wegen der Doppelschleife), es besteht aber Hoffnung nur knapp über linear zu landen, weil die zweite Schleife vorzeitig abgebrochen wird.
Funktionale Lösung
Die direkte Übernahme dieses Ansatzes in eine funktionale Programmiersprache wie Haskell ist trivial:
import System.Environment
squares = [ i*i | i <- [ 1 .. ] ]
winners :: [Bool]
winners = False : [ and [ not $ winners !! (i-x)
| x <- takeWhile (<= i) squares
]
| i <- [1 .. ]
]
main = do [c] <- getArgs
count <- readIO c
print (winners !! count)Man baut sich also eine unendliche Liste der möglichen Offsets (Quadrate). Mit der bastelt man die unendliche Liste der Gewinnerwerte zusammen, indem man beim Aufbau auf die Liste selbst zurückgreift. Das funktioniert, weil man nur auf Werte zugreift, die schon berechnet werden konnten.
Von der Liste gibt man das entsprechende Element zurück.
Unglücklicherweise ist das ziemlich langsam, denn die Doppelschleife ist eigentlich eine Dreifachschleife. Die Datenstruktur "[]" ist eine einfach verkettete Liste, die der "!!"-Operator immer von Anfang an durchlaufen muss.
Und genau das Problem habe ich in einem anderen Kontext auch. Also muss da eine Lösung her.
Effizientere Implementierung
Um die ständigen Rücksprünge zu vermeiden, kann man die Tatsache ausnutzen, dass man eigentlich mit mehreren Indizes (um Quadrate versetzt) linear durch die Liste durchläuft.
winners :: [Bool]
winners = False : worker 1 squares []
where
worker i so@(s:sn) rs
| s == i = worker' i sn (winners:rs)
| otherwise = worker' i so rs
worker' i ss rs = and (map (not . head) rs)
: worker (i+1) ss (map tail rs)Die Implementierung besteht also darin, mitzuzählen und jedes mal, wenn man eine Quadratzahl erreicht hat, einen weiteren Runner über das bisherige Feld aufzunehmen. Das macht die Teilfunktion worker.
Die eigentliche Wertermittlung erfolgt in der Teilfunktion worker', die von allen Runnern das erste Element auswertet und mit den Resten in die nächste Iteration läuft.
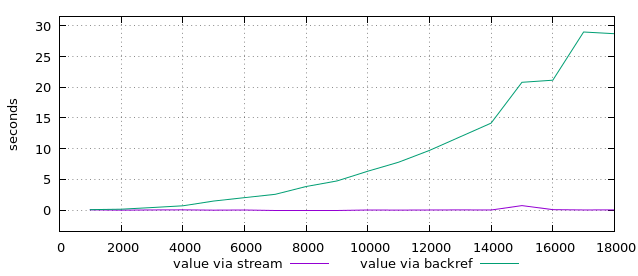
Ein direkter Vergleich der Laufzeiten zeigt einen durchschlagenden Erfolg:
Seltsame Spitzen
Ungewöhnlich sind die Spitzen der violetten Kurve in diesem Graphen. Wo kommen die her? Fehlmessungen?
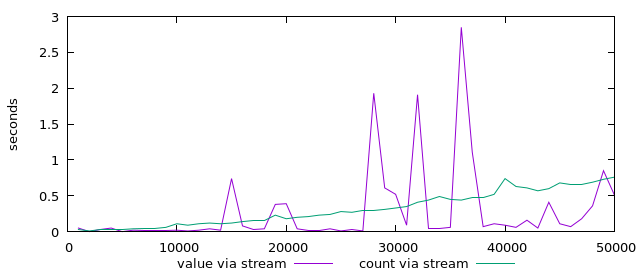
Also lass ich weitere Werte berechnen und sehe, dass die Spitzen bleiben. (Den Teil mit dem count ignoriere man mal vorerst.)
Nun gut, es mag an der Schrittweite liegen, denn ich nehme nur alle 1000 Werte einen Messpunkt. Also mal in Einzelschritten in ein solches Intervall hinein hüpfen:
Auch hier zeigt die violette Kurve ein extrem zackiges Bild. Warum?
Weil Haskell faul ist. Lazy evaluation ist eine Eigenschaft von Haskell, nur dann einen Wert auszurechnen, wenn der auch gebraucht wird.
In diesem Fall lautet die Aufgabe, einen bestimmten Wert in einer Liste auszugeben. Dazu geht Haskell die Listenkonstruktion durch und stellt fest, dass in jeder Iteration ein neues Element erzeugt wird. (In worker')
Um den konkreten Wert dann doch zu ermitteln, geht Haskell die Berechnung an und beginnt mit dem letzten hinzugefügten Runner. Der steht aber am Anfang der Liste und mit etwas Glück erwischt er gleich einen Abbruchwert. Damit kann Haskell das Ergebnis ausgeben und ist fertig.
Nur, wenn das Spiel wirklich eine komplexere Situation zu bewerten hat, muss Haskell deutlich mehr berechnen.
Um ihn zu zwingen, alle Werte zu ermitteln lasse ich die Anzahl der Gewinnzahlen bis zu der angefragten Position zu ermitteln.
-- print $ winners !! count
print . length . filter id . take count $ winnersEine alternative Formulierung wäre:
print $ length [ x | x <- take count winners , x ]
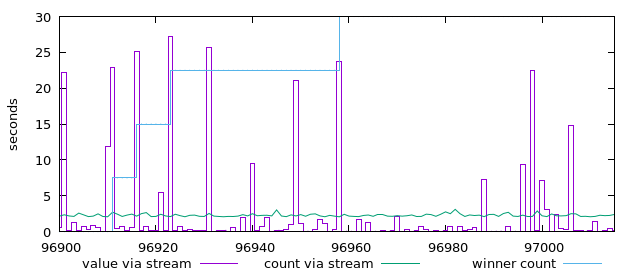
Das Ergebnis ist verblüffend. Es ist genau die grüne count-Kurve in den oben stehenden Diagrammen.
Immer, wenn ein neuer Gewinnwert dazu kommt (oder in kleinen Schritten erreichbar wäre), steigt die Rechenzeit deutlich an. Das ist an der überlagerten blauen Stufenkurve zu sehen.
Als Gegentest kann man die Konstruktion "(winners:xs)" in worker durch "(xs ++ [winners])" ersetzen und zuerst den Wert des direkten Vorgängers benutzen. Das stellt ebenfalls sicher, dass alle Werte ermittelt werden. Die Laufzeiten liegen dann in vergleichbaren Größenordnungen wie beim count-Fall.
Warum dauert die Abarbeitung in Einzelfällen aber deutlich länger als im count-Fall? Er hat doch eigentlich weniger zu berechnen?
Die von Haskell zurückgelegten Teilberechnungen sind eine teuere Angelegenheit, sie anzulegen und später auszurechnen kostet deutlich mehr Zeit (und Speicher) als direkt zur Rechnung zu schreiten.
Nochmal!
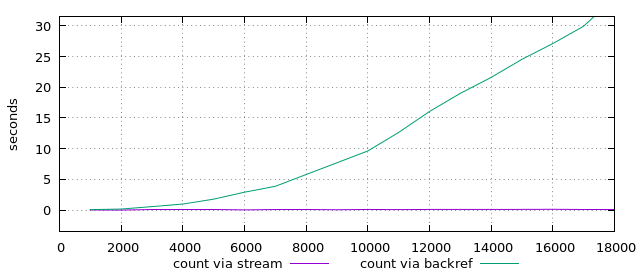
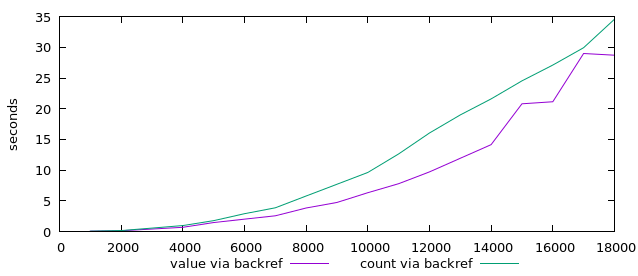
Mit diesen Erkenntnissen vergleiche ich jetzt nochmal die beiden Algorithmen: Backreferenz per "!!"-Operator und mehrere Stream-Runner. Allerdings berechne ich diesmal die Anzahl der Gewinnzahlen.
Auch hier ist der Vergleich ähnlich: Die Runner gewinnen deutlich.
Evtl. hat ja die count-Berechnung auch das andere Verfahren massiv verlangsamt? Also beide Laufzeiten im direkten Vergleich:
Die Backreferenz-Methode benötigt auch dann viel Zeit, wenn sie gar nicht alle Werte berechnen muss. Die Berechnung aller Werte dauert aber konstant länger. Beide Laufzeiten sind aber vergleichbar.
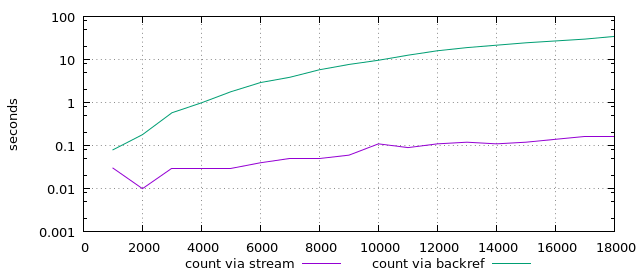
Zum Abschluss noch der direkte Vergleich der Methoden in der logarithmischen Darstellung:
Die Backreferenz-Methode ist klar polynomial (vermutlich O(n3)) während die Stream-Methode noch exponentiell aussieht (was sie aber nicht ist).
Fazit
Man achte bei der Programmierung stets darauf, ob der Algorithmus zum Programmumgebung passt.
Ist das nicht der Fall, verschlechtern sich die Ergebnisse erheblich. Dann muss entweder der Algorithmus (Streams statt Backreferenzen) oder die Umgebung (Data.Array statt Listen) angepasst werden.
Will man die Vorteile der Programmumgebung (Lazy Evaluation) erhalten, muss man die gewohnten algorithmischen Bahnen verlassen.
Als Belohnung winkt eine überdurchschnittliche Performance.

Ansonsten: Schönes Beispiel, vielen Dank! Ich bin immer noch in der Haskell-Anfängerphase und wäre auf den Ansatz im Leben nicht gekommen.
1 Kommentare