Wie schnell sind Algorithmen in Haskell? - Vorbereitungen
Haskell ist derartig faul, dass die gängigen Methoden zur Abschätzung der Programmlaufzeit scheitern. Nach der bahnbrechenden Arbeit von Okasaki bestand aber Hoffnung, dieses Thema in den Griff zu bekommen. Einige der Annahmen dieser Arbeit sind nicht anwendbar, wenn Haskell selbst zum Aufräumen von Zwischenergebnissen zu faul ist. Um selbst einige Ideen auszuprobieren, brauche ich reale Messwerte. Und die will ich jetzt erzeugen.
Profiling
Der klassische Weg mit Performance Problemen umzugehen, ist Profiling. Als Beispiel muss wieder die Fibonacci-Folge herhalten. Und das besonders ineffizient:
fib :: Int -> Int fib 0 = 1 fib 1 = 1 fib n = a + b where a = fib (n-1) b = fib (n-2)
Ich habe die Zwischen-Terme a und b extra benannt, damit sie im Profiling dann auch auftauchen.
Ich möchte die Zeit messen, die Haskell zur Abarbeitung braucht, dazu lasse ich mir die verstrichene CPU Zeit vor und nach der Abarbeitung geben. Um das Programm mit verschiedenen Werten zu testen, lese ich das Argument der Funktion von der Kommando-Zeile ein.
import System.Environment import System.CPUTime main = do [arg] <- getArgs limit <- readIO arg print limit start <- getCPUTime let result = fib limit finish <- getCPUTime print (finish - start) -- picoseconds
Nun noch kompilieren und probieren:
$ ghc -O3 -prof -fprof-auto -rtsopts fib.hs [1 of 1] Compiling Main ( fib.hs, fib.o ) Linking fib ... $ fib 20 20 14000000 $ fib 200 200 14000000
Huch? Warum sollte das Programm die gleiche Zeit brauchen, wenn es doch so unterschiedliche Berechnungen zu vollführen hat? Die angegebene Zeit ist in Picosekunden, also stehen da real 14µs. Etwas wenig.
Schauen wir mal in das Profiling:
$ fib 200 +RTS -p
200
5000000
$ cat fib.prof
individual inherited
COST CENTRE MODULE no. entries %time %alloc %time %alloc
MAIN MAIN 54 0 0.0 1.1 0.0 100.0
CAF Main 107 0 0.0 0.1 0.0 2.2
main Main 108 1 0.0 0.0 0.0 0.0
CAF GHC.IO.Encoding 95 0 0.0 5.5 0.0 5.5
CAF GHC.IO.Handle.FD 92 0 0.0 56.5 0.0 56.5
CAF GHC.IO.Handle.Text 91 0 0.0 0.1 0.0 0.1
CAF Text.Read.Lex 88 0 0.0 1.1 0.0 1.1
CAF GHC.IO.Encoding.Ic 83 0 0.0 0.4 0.0 0.4
CAF GHC.Conc.Signal 73 0 0.0 1.0 0.0 1.0
CAF GHC.Read 68 0 0.0 1.5 0.0 1.5
main Main 109 0 0.0 30.5 0.0 30.5Man sieht sehr schön. dass die übergebene Zahl vom Lexer bearbeitet, Daten ausgegeben wurden. Was aber komplett fehlt, ist jedoch die Abarbeitung der fib-Funktion?
Haskell ist schlicht zu faul, die Berechnung überhaupt auszuführen, wenn sowieso niemand das Ergebnis braucht! Um dem abzuhelfen, muss man das Ergebnis also auch noch ausgeben.
main = do [arg] <- getArgs limit <- readIO arg print limit start <- getCPUTime let result = fib limit finish <- getCPUTime print (finish - start) print result
Einfach am Ende noch das Ergebnis ausgeben. Sollte tun, oder?
$ fib 35 35 9000000 [ ... Pause ...] 14930352
Das Ergebnis erscheint mit deutlicher Verzögerung nach der Ausgabe. Insofern sind die angegebenen 9µs definitiv unpassend. Was ist passiert?
Haskell war zu faul, das Ergebnis sofort zu berechnen. Erst als es durch die Ausgabe gezwungen wurde, hat es die Berechnung nachgeholt. Da war die Zeitmessung allerdings schon lange vorbei.
Die Verwendung des Ergebnisses muss also vor dem Ende der Zeitmessung erfolgen!
main = do [arg] <- getArgs limit <- readIO arg print limit start <- getCPUTime let result = fib limit print result finish <- getCPUTime print (finish - start)
Und das gibt:
$ fib 35 +RTS -p 35 14930352 1354134000000
Jetzt zeigt die Zeitmessung auch passende 1,3 Sekunden. Und was sagt das Profilinging?
individual inherited
COST CENTRE MODULE entries %time %alloc %time %alloc
MAIN MAIN 0 0.0 1.1 100.0 100.0
CAF Main 0 0.0 0.0 0.0 2.1
main Main 1 0.0 2.0 0.0 2.0
CAF GHC.IO.Encoding 0 0.0 5.4 0.0 5.4
CAF GHC.IO.Handle.FD 0 0.0 54.6 0.0 54.6
CAF GHC.IO.Handle.Text 0 0.0 0.1 0.0 0.1
CAF Text.Read.Lex 0 0.0 1.1 0.0 1.1
CAF GHC.IO.Encoding.Iconv 0 0.1 0.4 0.1 0.4
CAF GHC.Conc.Signal 0 0.0 1.0 0.0 1.0
CAF GHC.Read 0 0.0 1.5 0.0 1.5
main Main 0 0.0 32.8 99.9 32.8
main.result Main 1 0.0 0.0 99.9 0.0
fib Main 29860703 28.3 0.0 99.9 0.0
fib.a Main 14930351 40.8 0.0 40.8 0.0
fib.b Main 14930351 30.8 0.0 30.8 0.0Die eine Zahl Differenz zwischen a und b macht allein 10% der benötigten Rechenleistung aus. Das ist beachtlich.
Zeitverhalten
Zurück zum urspünglichen Problem: Wie schnell sind Algorithmen in Haskell? Die Frage bezieht sich normalerweise auf die Entwicklung des Zeitverhaltens in Abhängigkeit von der zu verarbeitenden Datenmenge.
Grundsätzlich könnte man das bisherige Programm für jeden Zahlenwert einzeln aufrufen und die Zeiten aufschreiben. Aber das ist aufwändig und kann von Haskell selbst gemacht werden.
Zunächst einmal ist zuverlässig sicher zu stellen, dass der Versuch der Berechnung nicht über alle Zeiten hinauswächst. Die Berechnung muss notfalls abgebrochen werden. Das löst die Funktion System.Timeout.timeout: Sie lässt die Berechnung in parallelen Thread laufen und bricht den notfalls ab. Das ganze Signalisierungsverhalten ist zwar prinzipell einfach, aber die Bibliotheksfunktion löst auch die kleinen Dreckeffekte, über die man selbst noch nicht gestolpert ist.
Anderseits ist der bisherige Rückgabewerte von CPUTime schwer verständlich. Besser wäre ein klarer Wert ins Sekunden. Deswegen wechsle ich hier auf Data.Time.getCurrentTime.
Der dritte Punkt, der zu beachten ist, behandelt die vollständige Evaluierung der Eingabedaten vor der Ausführung der zu testenden Funktion, sowie das Erzwingen der notwendigen Berechnung. Dazu verlange ich zwei Hilfsfunktionen: pre dient dazu, aus dem numerischen Wert der Datenmenge auch brauchbare Ausgangsdaten zu erzeugen, z.B. eine Baumstruktur, über die der Algorithmus dann laufen soll. post dagegen extrahiert aus dem Ergebnis des Algorithmus eine Zahl. Diese Extraktion muss nicht zwingend alle Teile des Ergebnisses auswerten, es genügt z.B. die Länge eines Rückgabestrings zu ermitteln, wenn es sich um einen Algorithmus zur Stringverarbeitung handelt, schließlich sind die konkreten Inhalte des Strings dabei nicht relevant.
Die Eingabedaten werden komplett angezeigt, um alle Details zu evaluieren. Zum Erzwingen der Auswertung an der richtigen Stelle werden die Zahlenwerte auf positive Wertebereiche per Control.Monad.guard geprüft.
import Data.Time import Control.Monad profile :: (Show a) => (a -> b) -> (Int -> a) -> (b -> Int) -> Int -> IO (Maybe NominalDiffTime) profile test pre post n = do let input = pre n guard $ 0 <= length (show input) -- fully evaluate before measuring timeout 5000000 (do start <- getCurrentTime let output = test input guard $ 0 <= post output -- evaluate the relevant part finish <- getCurrentTime return $ finish `diffUTCTime` start )
Nochmal in Worten:
- Die Funktion pre macht aus einem Zahlenwert die Datenstruktur a, auf der der Algorithmus arbeiten soll.
- Die Funktoin test führt den Algorithmus aus, in dem sie als Argument eine Datenstruktur a übergeben bekommt und eine Datenstruktur b zurück liefert.
- Die Funktion post presst aus der Ergebnisstruktur b einen positiven Zahlenwert heraus, wobei sie die Ausführung des Algorithmus erzwingt.
- Klappt alles, erhalten wir die Zeit, die die Funktionen test und post benötigt haben.
- Die Berechnung ist mit einem Timeout von 5 Sekunden umschlossen: Endet die Berechnung nicht rechtzeitig gibt es Nothing.
Mit einer solche Mess-Funktion kann man nun eine Mess-Reihe automatisch erzeugen:
mkProfile :: (Show a) => (a -> b) -> (Int -> a) -> (b -> Int) -> IO () mkProfile test pre post = worker (profile test pre post) testpoints where testpoints = [ 1 .. 9 ] ++ [ x*10^c | c <- [0 .. ], x <- [10 .. 99] ] worker f (x:xs) = do r <- f x case r of (Just y) -> do putStrLn . shows x . showChar ',' . init $ show y when (y < 5) $ worker f xs _ -> putStrLn "# Timed out"
Für eine Reihe von Testpunkten, die immer größere Abstände annehmen, wird die Laufzeit ermittelt. Da die Darstellung der Laufzeit ein finales "s" für Sekunden am Ende hat, wird es per init abgeschnitten. Der Rest der Ausgabe ist ein CSV.
Die Messung wird fortgeführt, wenn überhaupt ein Ergebnis ermittelt werden konnte (kein Timeout) und die Laufzeit die 5 Sekunden nicht überschreitet. Die Timeout-Funktion garantiert nur, dass der Abbruch nicht vor 5 Sekunden stattfindet. Länger kann es durchaus dauern, da die typische Haskell-Runtime kooperatives Multitasking betreibt.
Und was sagt das zu unserer Fibonacci-Folge?
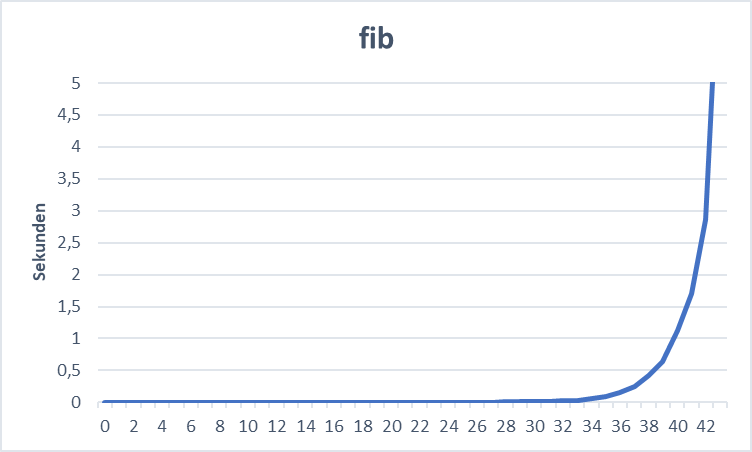
main = mkProfile fib id id
Die Hauptfunktion ist denkbar einfach: Erstelle ein Profil der fib-Funktion, wobei die Eingabemenge aus der Zahl besteht, die übergeben wird. Das Ergebnis ist ebenfalls eine Zahl, die so übernommen wird wie sie ist.
Das ist klar expotentielles Wachstum.
Damit steht nun ein Handwerkszeug zur Verfügung, um andere - interessantere Algorithmen - zu untersuchen.
Nachbetrachtung
Natürlich würde man die Fibonacci-Folge in Haskell niemals so schreiben, sondern eher so:
fibs = 1 : 1 : zipWith (+) fibs (tail fibs) fib1 x = fibs !! x main = mkProfile fib1 id abs
Die Fibonacci-Folge besteht aus den Werten 1, 1 und dann der Summe der Fibonacci-Werte beginnend am Anfang und um ein Element versetzt. Die Liste ist unendlich lang, aber dank des faulen Haskells besteht da kein Problem: Denn nur der x-te Wert wird dann heraus genommen.
Da wir mit Int rechnen, gibt es Überläufe während der Rechnung. Anstatt auf den korrekten Typ Integer auszuweichen, nehme ich hier einfach den Absolutwert als Ergebnis. Es geht ja nicht um die Berechnung der Werte an sich, sondern um die Art der Ermittlung (also den Algorithmus).
Und das ergibt dann?
Das ist spannend! Mit einigen Ausreißern geht die Berechnung fast linear durch und zwar in die zig Millionen, statt bis 42.
Beobachtet man allerdings den RAM-Verbrauch während der Abarbeitung, so steigt dieser bis zu 4 GB an (mehr gebe ich dem Prozess hier nicht). Dann bricht die Abarbeitung ab. Die Stellen, bei denen die Laufzeit so stark ansteigt, entspricht den Stellen, wo das System massiv nach RAM verlangt.
Was ist passiert?
Die Definition von fibs ist global, d.h. der Wert steht immer zur Verfügung. Anders gesagt, verwirft Haskell die ermittelten Werte des Feldes nie wieder. Deswegen steigt der RAM-Verbrauch immer weiter an. Am Ende sind über 40 Mio. Werte berechnet worden. Incl. Overhead für die verkettete Liste sind das also ungefähr 80 Byte pro Eintrag.
Andererseits führt das zu den niedrigen Laufzeiten, da ja alle Werte schon berechnet wurden.
Alle Werte? Nein, die Schrittweite steigt ja immer um eine Größenordung. Damit müssen auch immer mehr Zwischenwerte berechnet werden, um auf das nächste Ergebnis zu kommen. Dies erklärt die sprunghaft steigende Abarbeitungszeit, die mit der größeren Schrittweite korreliert.
Was wäre nun, wenn man korrekterweise nicht mit den übrig gebliebenen Berechnungen des vorherigen Versuchen zu betrügen versucht?
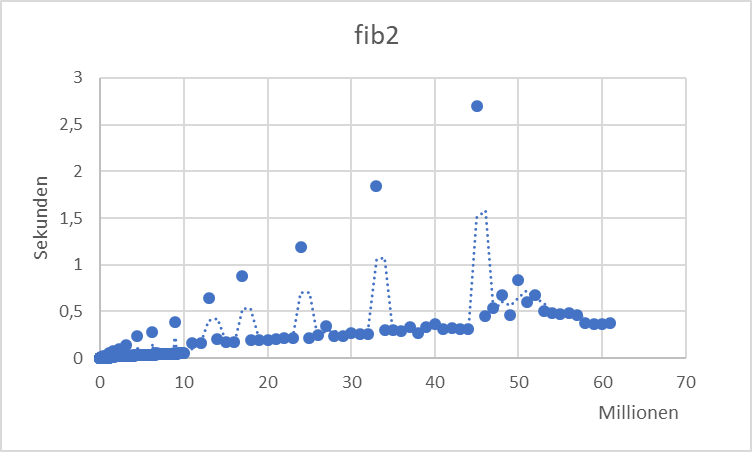
fib2 x = fib' !! x where fib' = 1 : 1 : zipWith (+) fib' (tail fib')
Hier werden die Zwischenergebnisse in einer lokalen Variablen gehalten, die außerhalb des Aufrufs keine Bedeutung hat. Es besteht sogar die Hoffnung, dass die nicht benötigten Zwischenergebnisse direkt verworfen werden, und so der RAM-Bedarf nicht exorbitant steigt.
Zwei Dinge sind auffällig:
- Der RAM-Bedarf steigt wieder so an, das Programm hält aber länger durch, wenn die Grenze erreicht ist.
- Das Laufzeitverhalten ist ähnlich, erreicht aber deutlich höhere Werte.
Was ist passiert?
Haskell erkennt durchaus, dass die Definition von fib' unabhängig vom Aufrufparameter ist und benutzt diese Tatsache zu dem Memorization-Trick, der bei fibs noch explizit aufgeschrieben wurde. Das führt zu dem ähnlichen Verhalten bis zu 40 Mio. Danach muss (und kann) Haskell die Zwischenergebnisse immer wieder verwerfen, um weiter arbeiten zu können.
Kann man Haskell den Algorithmus expliziter vermitteln? Schließlich ist es ja wenig elegant, eine Liste von uninteressanten Werten jedesmal von Anfang an zu durchlaufen (was schonmal minimal lineare Laufzeit generiert)
fib3 x = head $ drop x fib' where fib' = 1 : 1 : zipWith (+) fib' (tail fib')
Der einzige Unterschied ist hier, dass statt dem (!!) Operator, der eine Liste bis zum x-ten Element durchläuft, der Anfang der Liste weggeworfen wird, um dann das erste Element zu nehmen.
Das gleiche Bild, allerdings sind die Laufzeiten kürzer und die Abarbeitung erfolgt glatter. Es ist nicht so erratisch. Das exorbitante RAM-Bedarf ist allerdings noh da.
Also muss auf die Liste als solche verzichtet werden.
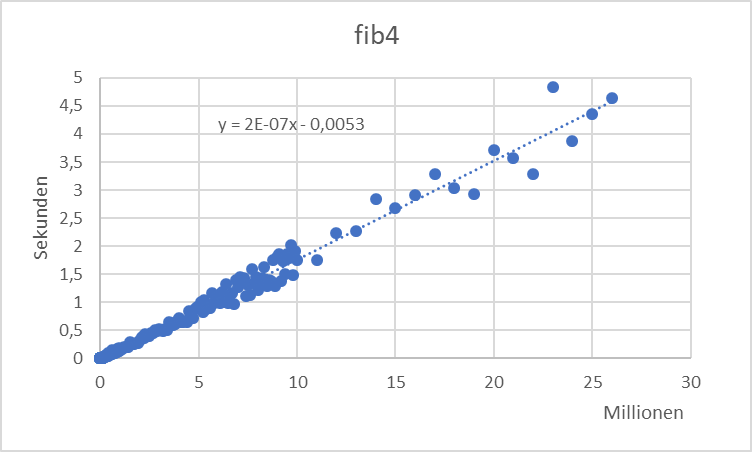
fib4 x = fib' x (1,1) where fib' 0 (a,_) = a fib' n (a,b) = fib' (n-1) (b,a+b)
Dieses Programm nimmt den Kern der zipWith (+) Funktion explizit her und zählt parallel rückwärts. Es sammelt die Werte gar nicht erst auf, sondern verwirft sie sofort.
Der RAM-Bedarf ist diesmal konstant. Das ist allerdings erwartungskonform.
Eine echte Überraschung ist allerdings die Laufzeit dieses Algorithmus:
- Die Laufzeit ist praktisch linear mit 2 Sekunden je 10 Mio.
- Allerdings sind die anderen Algorithmen durch die Bank deutlich schneller als die direkte Berechnung der Werte.
| Mio | fib1 | fib2 | fib3 | fib4 |
| 10 | 53ms | 53ms | 52ms | 1750ms |
| 20 | 192ms | 189ms | 189ms | 3714ms |
| 30 | 349ms | 264ms | 238ms | |
| 40 | 321ms | 361ms | 298ms | |
| 50 | 839ms | 339ms | ||
| 60 | 366ms | 365ms |
Fazit
Die von Haskell angewendeten Methoden der Memorization gestatten es, perfomante Algorithmen zu schreiben, die im Gegensatz zu den klassischen Algorithmen geschickter betrügen. Man muss bei Performance Messungen also höllisch aufpassen.