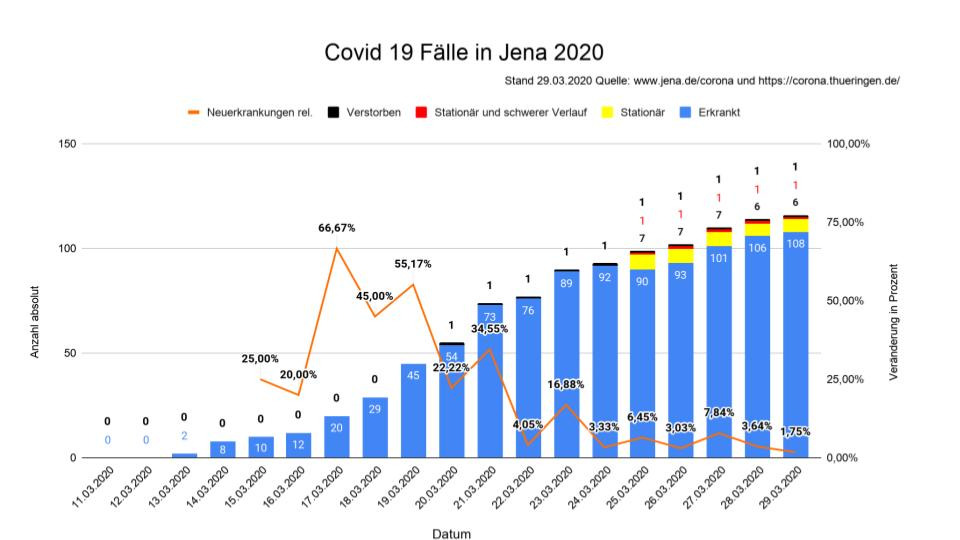
Sind 3% Zuwachs bei den Fallzahlen gut oder schlecht?
Wir sind Zombies geworden, sitzen daheim und starren auf Zahlen, auf Bilder. Geht es aufwärts? Geht es abwärts? Wann ist es vorbei?
Nehmen wir das Bild, das Bastian Stein regelmäßig aktualisiert:
Schon beim Betrachten des Bildes hat man ein gutes Gefühl. Der Zuwachs ist nicht mehr so steil! Wir schwanken nur noch um einstellige Zuwachsraten! Die Verfügungen der Stadt Jena zeigen nach knapp zwei Wochen tatsächlich Wirkung!
Oder etwa doch nicht?
Was heißt eigentlich, 3% Zuwachs jeden Tag?
Mathematisch gesehen ist der Zuwachs die Ableitung, d.h. f(x)' = 0.03 * f(x).
Und die Lösung dazu lautet f(x) = e0.03 x
Au, weh! Da ist ja die gefürchtete Exponentialfunktion!
Wenn wir schon mal hier sind, fragen wir nach der Verdopplungszeit. Dies ist die Zeit, in der sich die Fallzahlen verdoppeln, also f(x+d) = f(x) * f(d) = f(x) * 2. Also ist f(d) = ed*0.03 = 2.
Die Verdopplungszeit in Jena ist demzufolge d = log(2) / 0.03 = 23,1 d. Damit sind wir in Jena aktuell besser als Südkorea (14,8 d).
Woran erkennt man nun, ob es wirklich besser wird?
Zum einen fehlen komplett die Genesenen (oder Verstorbenen), denn die Krankheit dauert ja im Schnitt nur zwei Wochen. Die Anzahl der aktuell Infizierten ist also um die Anzahl niedriger, die schon vor 14 Tagen krank waren. Damit haben wir in Jena heute erstmals einen Rückgang in der Anzahl der Infizierten, denn die 10 vom 15.3. können als Genesen angesehen werden. Trotzdem ändert das allein nichts am exponentiellen Anstieg.
Diese Personen fallen aus der Menge der Infizierbaren heraus. Selbst wenn sie sich frei bewegen, denn sie sind immun und übertragen sie die Krankheit nicht mehr. Diejenigen, die noch infizierbar sind, müssen noch solange die Immunität simulieren, indem sie daheim bleiben. Das ist der Kern der Ausgangsbeschränkungen.
Je mehr Menschen Immunität erreichen, desto lockerer können die Beschränkungen sein. Einige Zeit (ein oder zwei Wochen) nach Überschreiten des Peaks kann man die Ausgangsbeschränkungen lockern. Man muss gegebenenfalls nachjustieren und immer mal wieder für einige Zeit immer lockere Ausgangsbeschränkungen verhängen, um die Belastung des Gesundheitssystems unter dem Limit zu halten. Die genaue Ausgestaltung ist das Exit-Szenario.
Anderseits gibt es nur endlich viele Menschen, die sich infizieren können. So verschiebt sich nach und nach das Verhältnis der Immunen zur Gesamtbevölkerung. Ab 60 bis 70% geht man von Herdenimmunität aus. Der benötigte Wert ergibt sich primär aus der Ansteckungsrate.
Wie sich die Zahlen für die Infizierten entwickeln, kann man mit dem SIR Modell prognostizieren. Wie das für verschiedene Länder und Bundesländer aussieht, kann man mit aktuellen Zahlen hier nachschauen.
Interessant ist die maximale Zahl der Infizieren. Für Deutschland rechnet das Modell für den 6. Mai 2020 mit einem Maximum von 5,2 Mio. Infizierten, also vielleicht 700.000 schweren Fällen. Die Kapazität in Deutschland liegt bei 28.000 Intensivbetten, davon sind 6000 aktuell nicht belegt. Hier liegt absehbar eine Überlastung des Gesundheitssystems vor.
Gibt man alle Werte in eine entsprechende Simulation ein, so bekommt man
- ohne Ausgangsbeschränkung für Jena ein Bedarf an 7000 Intensivbetten Ende Mai.
- mit aktueller Ausgangsbeschränkung in Jena ein Bedarf an 70 Intensivbetten Ende April.
Die 3% sind schön, aber nicht ausreichend. Der Wert muss fallen, die Neuinfektionen dürfen nur linear wachsen, besser konstant bleiben oder fallen.
Das sind bloß keine Fälle, sondern positive Testergebnisse. Was würden wir wohl jemandem sagen, der statt der Geburtenrate die Anzahl der positiven Schwangerschaftstests als relevante Zahlen verkauft und täglich berichtet - wobei Männer, Kinder und Greise fleißig mitgetestet werden?
Dabei ermittelt die AGI am RKI seit vielen Jahren stichprobenartig die tatsächliche Anzahl der Atemwegserkrankungen und da sieht man zu Beginn von Corona absolut normale Zahlen und dann mit dem Lockdown einbrechende Zahlen (vermutlich, weil sich die Leute nicht mehr zum Arzt trauen):
https://influenza.rki.de/Wochenberichte.aspx
Yeti
PS. Bei kleinen Werten für r ist der Fehler überraschend klein - bei r=3% beträgt die korrekte Verdoppelungszeit ca. 23.5 Tage statt 23.1.
Total 3 comments